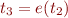Table des matières
Au départ ce billet était un article de vulgarisation, qui s'est transformé en brouillon de recherche au fur et à mesure que j'avançais mes idées et que je découvrais celles des autres. Il mériterait une refonte, quand j'en prendrai le temps.
Introduction
Il y a beaucoup à dire historiquement sur le sujet, et je referai probablement l'article après l'avoir croisé avec des articles intéressants comme Science étonnante ou Science4All, et surtout il faudrait que je lise l'ouvrage de référence de Hardy. Mais pour l'instant je souhaitais juste mettre au propre mes premières réflexions sur le sujet…
Séries convergentes
Comme il y a déjà beaucoup à dire1), je vais partir du principe que les sommes infinies comme
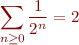
ne vous font pas peur. Si c'est bien le cas, vous savez alors qu'on dit qu'une série  est dite convergente si la suite des sommes partielles est finie :
est dite convergente si la suite des sommes partielles est finie :
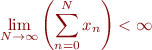
C'est le cas par exemple de 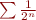 , puisque :
, puisque :
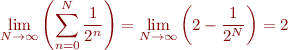
Astuce : le calcul entre parenthèses est obtenu de façon générale pour toutes les séries géométriques, c'est à dire les séries de la forme 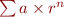 :
:
![Equation $$\[\begin{array}{r@{}l}
(1 - r) \times (a + ar + ar^2 + \dots + ar^N) &{} = (a + ar + ar^2 + \dots + ar^N)\\
&{} \hspace{0.665cm} - (ar + ar^2 + \dots + ar^N + ar^{N+1})\\
&{} = a - ar^{N+1}\\
\end{array}\]$$](/lib/exe/fetch.php?media=wiki:latex:/img795e794d205bc6d796db0b45d4ab8ea5.png)
Donc si la raison  de la suite est différente de
de la suite est différente de  , nous avons :
, nous avons :
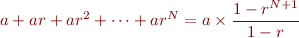
Donc en remplaçant  et
et 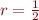 dans l'expression, nous avons bien :
dans l'expression, nous avons bien :
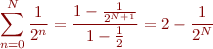
En généralisant le raisonnement précédent (exercice ^^), on s'aperçoit que les séries géométriques sont convergentes si et seulement si  .
.
Une série qui n'est pas convergente sera dite divergente. La question du jour est : peut-on quand même attribuer de manière raisonnable une valeur à des suites divergentes ?
Principes
J'ai pris le temps de discuter des séries géométriques car elles sont un exemple simple des opérations que l'on souhaite faire sur les séries. Nous avons obtenu  implicitement en réorganisant les termes, ce qui fonctionne bien s'il y a un nombre fini de termes, mais pas s'il y en a une infinité. Prenons la série suivante :
implicitement en réorganisant les termes, ce qui fonctionne bien s'il y a un nombre fini de termes, mais pas s'il y en a une infinité. Prenons la série suivante :
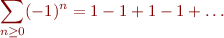
Il est possible de la parenthéser de deux manières différentes pour obtenir une contradiction :
![Equation $$\[\begin{array}{r@{}l}
\sum\limits_{n \ge 0}(-1)^n &{} = (1 -1) +(1 -1) + \dots\\
&{} = 0 + 0 + \dots\\
&{} = 0\\
\end{array}\]$$](/lib/exe/fetch.php?media=wiki:latex:/imgcd8af5dca6773fc67a262c516b17d1f4.png)
![Equation $$\[\begin{array}{r@{}l}
\sum\limits_{n \ge 0}(-1)^n &{} = 1 + (-1 +1) + (-1 +1) + \dots\\
&{} = 1 + 0 + 0 + \dots\\
&{} = 1\\
\end{array}\]$$](/lib/exe/fetch.php?media=wiki:latex:/imgd7d4c10b8438b4c42561ebf3b272a88a.png)
L'idée est donc de trouver un ensemble d'opérations sur les séries divergentes qui permette de trouver des valeurs pertinentes sans qu'il y ait contradiction. Comme nous voulons généraliser le travail déjà fait sur les séries convergentes, la moindre des choses serait que si nous appliquons nos opérations sur des séries convergentes, nous obtenions la même valeur qu'avec les sommes partielles. C'est l'axiome de régularité :
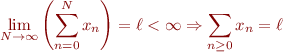
Notez que j'utilise le même symbole  pour la sommation classique et notre sommation sur les séries en général même si elles sont divergentes. En fait, nous cherchons une extension cohérente de
pour la sommation classique et notre sommation sur les séries en général même si elles sont divergentes. En fait, nous cherchons une extension cohérente de  , et il serait plus rigoureux de le noter autrement, par exemple
, et il serait plus rigoureux de le noter autrement, par exemple  . Mais nous ne voulons pas alourdir les notations par la suite, et si jamais nous parvenons au but à cause de l'axiome de régularité nous pourrons confondre les deux symboles.
. Mais nous ne voulons pas alourdir les notations par la suite, et si jamais nous parvenons au but à cause de l'axiome de régularité nous pourrons confondre les deux symboles.
Nous avons vu que nous ne pouvions pas parenthéser les séries divergentes n'importe comment. Par la suite nous ne nous autoriserons qu'une seule réorganisation de terme : pouvoir extraire le premier terme. C'est à dire que nous respectons une structure de liste pour les séries, afin de correspondre à l'intuition de « pou obtenir le résultat, j'additionne le premier terme, puis le second, puis le troisième, etc. ». Plus formellement, c'est l'axiome de stabilité, qui énonce que nous pouvons obtenir une (valeur pour) une nouvelle série  à partir d'une série
à partir d'une série  déjà définie telle que pour tout
déjà définie telle que pour tout  nous ayons
nous ayons  et
et 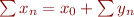 . Cela revient en fait à décaler la numérotation :
. Cela revient en fait à décaler la numérotation :
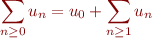
Rien qu'à ce stade, ça coince. En effet, prenons la série  :
:
![Equation $$\[\begin{array}{r@{}l}
\sum\limits_{n \ge 0}1 &{} = 1 +\sum_{n \ge 1}1\\
&{} = 1 +\sum_{n \ge 0}1\\
\end{array}\]$$](/lib/exe/fetch.php?media=wiki:latex:/img8f325c45c44194bd5cdd7ed7749285f2.png)
Donc en soustrayant  à gauche et à droite nous avons
à gauche et à droite nous avons  . Ainsi, il n'est pas possible d'appliquer notre méthode à toutes les séries, mais il est peut-être possible de restreindre le champ d'étude de façon à avoir des résultats cohérents… Je propose de nous limiter aux séries vérifiant que si elles sont périodiques alors la somme des éléments de la période vaut
. Ainsi, il n'est pas possible d'appliquer notre méthode à toutes les séries, mais il est peut-être possible de restreindre le champ d'étude de façon à avoir des résultats cohérents… Je propose de nous limiter aux séries vérifiant que si elles sont périodiques alors la somme des éléments de la période vaut  . Ainsi, nous éliminons
. Ainsi, nous éliminons  mais nous gardons
mais nous gardons  puisque
puisque  . Plus formellement :
. Plus formellement :
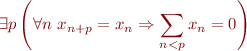
Pour faire des calculs pratiques nous souhaitons aussi munir considérer les séries comme un espace vectoriel, c'est à dire de nous autoriser à multiplier une série par un coefficient, et pouvoir faire la somme entre deux sorts. Plus formellement, c'est l'axiome de linéarité :
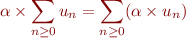
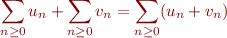
L'axiome de linéarité permet d'affaiblir l'axiome de régularité à seulement pouvoir ajouter un zéro en début de liste ?
En particulier, nous généralisons le raisonnement précédent sur les séries géométriques :
![Equation $$\[\begin{array}{r@{}ll}
\sum\limits_{n \ge 0}ar^n &{} = a + \sum\limits_{n \ge 1}ar^n&\text{(stabilité)}\\
&{} = a + \sum\limits_{n \ge 0}ar^{n+1}\\
&{} = a + r \times\sum\limits_{n \ge 0}ar^n &\text{(linéarité)}\\
\end{array}\]$$](/lib/exe/fetch.php?media=wiki:latex:/imgf84ebf9520d03ddffa78fc1b9fad9354.png)
Ainsi, en notant 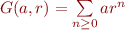 nous avons
nous avons  , d'où si
, d'où si  nous avons
nous avons 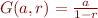 . Il est à noter que si
. Il est à noter que si  alors
alors  viole notre supposition sur la périodicité puisque nous retrouvons notre meilleure ennemie
viole notre supposition sur la périodicité puisque nous retrouvons notre meilleure ennemie 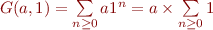 .
.
Le résultat 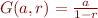 est effectivement le résultat obtenu pour les séries géométriques convergentes (pour
est effectivement le résultat obtenu pour les séries géométriques convergentes (pour  ), donc il vérifie la propriété de régularité. De façon amusante, comme
), donc il vérifie la propriété de régularité. De façon amusante, comme 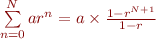 , cela revient à juste ignorer le terme infini pour la limite des sommes partielles.
, cela revient à juste ignorer le terme infini pour la limite des sommes partielles.
De plus, cette formule nous donne maintenant des résultats pour les séries géométriques divergentes (pour  ), par exemple pour
), par exemple pour  et
et  :
:
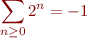
Une somme infinie d'entiers positifs donnerait un résultat négatif ?! Mais le pire est à venir, puisque notre but est de prouver que :
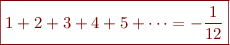
Quelques calculs
Pourquoi cette valeur, qui en plus d'être négative a le mauvais goût d'être une fraction ? ^^ Il y a des raisons physiques, voir par exemple l'article de Science Étonnante sur l'effet Casimir, mais ici je vais m'attarder sur les raisons mathématiques. Commençons plus doucement pour la Grandi 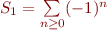 pour laquelle nous avions maladroitement donné les valeurs
pour laquelle nous avions maladroitement donné les valeurs  et
et  :
:
![Equation $$\[\begin{array}{r@{}l}
S_1
&{} = \sum\limits_{n \ge 0}(-1)^n\\
&{} = 1 + \sum\limits_{n \ge 1}(-1)^n\\
&{} = 1 + \sum\limits_{n \ge 0}(-1)^{n+1}\\
&{} = 1 - \sum\limits_{n \ge 0}(-1)^n\\
&{} = 1 - S_1\\
\end{array}\]$$](/lib/exe/fetch.php?media=wiki:latex:/img661bbafd00e57bb7c80d694cd07475c9.png)
Comme  donc la bonne valeur n'est pas
donc la bonne valeur n'est pas  ou
ou  , mais entre les deux :
, mais entre les deux :
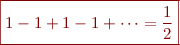
Passons à une autre : la série alternée des entiers 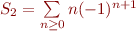 . En utilisant la série précédente, nous avons que :
. En utilisant la série précédente, nous avons que :
![Equation $$\[\begin{array}{r@{}l}
S_2 - S_1
&{} = \sum\limits_{n \ge 0}n(-1)^{n+1} - \sum\limits_{n \ge 0}(-1)^n\\
&{} = \sum\limits_{n \ge 0}\left(n(-1)^{n+1} - (-1)^n\right)\\
&{} = \sum\limits_{n \ge 0}(n+1)(-1)^{n+1}\\
&{} = \sum\limits_{n \ge 0}n(-1)^n\\
&{} = - S_2\\
\end{array}\]$$](/lib/exe/fetch.php?media=wiki:latex:/imga88aa8663e0ac4d4e3b7bca2553f227b.png)
Comme 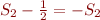 nous avons :
nous avons :
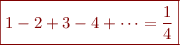
En passant, il est possible de définir le produit entre deux séries par :

par 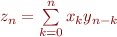 . Ainsi, une preuve alternative (mais dépassant nos règles précédentes) consiste à remarquer que le produit de
. Ainsi, une preuve alternative (mais dépassant nos règles précédentes) consiste à remarquer que le produit de  par lui-même donne une série avec les coefficients suivants :
par lui-même donne une série avec les coefficients suivants :
![Equation $$\[\begin{array}{r@{}l}
z_n
&{} = \sum\limits_{k = 0}^n(-1)^k(-1)^{n-k}\\
&{} = \sum\limits_{k = 0}^n(-1)^n\\
&{} = (n+1)(-1)^n\\
\end{array}\]$$](/lib/exe/fetch.php?media=wiki:latex:/imgc481f301caa13c447f1bac847f053faa.png)
Ainsi, la série obtenue par produit a comme valeur :
![Equation $$\[\begin{array}{r@{}l}
S_1 \times S_1
&{} = \sum\limits_{n \ge 0}(n+1)(-1)^n\\
&{} = \sum\limits_{n \ge 0}(n+1)(-1)^{n+2}\\
&{} = 0 + \sum\limits_{n \ge 1}n(-1)^{n+1}\\
&{} = \sum\limits_{n \ge 0}n(-1)^{n+1}\\
&{} = S_2\\
\end{array}\]$$](/lib/exe/fetch.php?media=wiki:latex:/img416d9642b3c8f7ee921f0cca2a36c049.png)
Ainsi, nous retrouvons par un autre moyen que 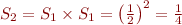 .
.
Note : ce serait plus élégant (et immédiat ^^') de la définir plutôt par : 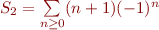
Notez que nous ne savons toujours pas si nos règles sont cohérentes, mais obtenir le même résultat par deux méthodes différentes est en soi rassurant. Passons maintenant à la somme des entiers naturels 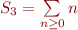 que nous essayons de résoudre par l'heuristique de Ramanujan. Mais pour cela nous avons besoin d'un dernier outil : la dilatation de série, c'est à dire le fait de pouvoir ajouter des zéros de façon homogène dans la série.
que nous essayons de résoudre par l'heuristique de Ramanujan. Mais pour cela nous avons besoin d'un dernier outil : la dilatation de série, c'est à dire le fait de pouvoir ajouter des zéros de façon homogène dans la série.
Ainsi, nous noterons 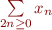 la série
la série 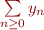 définie par :
définie par :
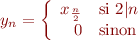
Nous admettrons momentanément que 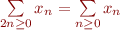 , c'est à dire que
, c'est à dire que  . Voilà le calcul proposé :
. Voilà le calcul proposé :
![Equation $$\[\begin{array}{r@{}l}
-3S_3
&{} = S_3 -4S_3\\
&{} = \sum\limits_{n \ge 0}n -4\sum\limits_{n \ge 0}n\\
&{} = \sum\limits_{n \ge 0}n -4\sum\limits_{2n \ge 0}n\\
&{} = \sum\limits_{n \ge 0}y_n\\
\end{array}\]$$](/lib/exe/fetch.php?media=wiki:latex:/img843b09627d25648ea8680f13b9451fb9.png)
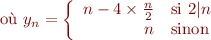
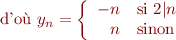
Ainsi, nous avons que :
![Equation $$\[\begin{array}{r@{}l}
-3S_3
&{} = \sum\limits_{n \ge 0}y_n\\
&{} = \sum\limits_{n \ge 0}n(-1)^{n+1}\\
&{} = S_2\\
\end{array}\]$$](/lib/exe/fetch.php?media=wiki:latex:/imgc6594d52ae02aa88023b379a1ce65ca2.png)
Donc 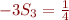 , et nous obtenons le résultat annoncé
, et nous obtenons le résultat annoncé 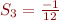 .
.
L'heuristique de Ramanujan serait plus clair de façon extensionnelle ?
Bon, oui et non, car nous avons quand même fait une hypothèse supplémentaire. En l'utilisant dans le calcul de  nous obtenons quelque chose d'inattendu :
nous obtenons quelque chose d'inattendu :
![Equation $$\[\begin{array}{r@{}l}
\frac{1}{2}
&{} = \sum\limits_{n \ge 0}(-1)^n\\
&{} = \sum\limits_{2n \ge 0}1 + \sum\limits_{2n+1 \ge 0}-1\\
&{} = \sum\limits_{2n \ge 0}1 + 0 + \sum\limits_{2n \ge 0}-1\\
&{} = \sum\limits_{n \ge 0}1 - \sum\limits_{n \ge 0}1\\
&{} = 0\\
\end{array}\]$$](/lib/exe/fetch.php?media=wiki:latex:/imgf0020b0177a7a9a880e779b9a0feea14.png)
Et revoilà notre meilleure ennemie 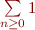 ! Ainsi, il semblerait qu'avec cette hypothèse les règles soient incohérentes…
! Ainsi, il semblerait qu'avec cette hypothèse les règles soient incohérentes…
Pour aboutir à une valeur, il faut utiliser la sommation de Ramanujan ?
Exercice : Montrer que  (alternance),
(alternance),  (?) et
(?) et 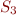 (petit Gauss) sont bien divergentes.
(petit Gauss) sont bien divergentes.
Somme et périodicité
En fait, même sans elle il serait possible d'écrire :
![Equation $$\[\begin{array}{r@{}l}
\frac{1}{2}
&{} = \sum\limits_{n \ge 0}(-1)^n\\
&{} = \sum\limits_{2n \ge 0}1 - \sum\limits_{2n \ge 0}1\\
&{} = 0\\
\end{array}\]$$](/lib/exe/fetch.php?media=wiki:latex:/imgd08dfe751c5a18f55655921ec7785355.png)
En fait, nous pouvons généraliser le raisonnement en définissant la notation 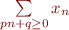 pour une période
pour une période  et un reste
et un reste 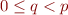 par la suite
par la suite 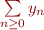 telle que :
telle que :
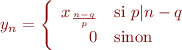
Remarquez que par stabilité, comme les premiers termes sont nuls nous avons pour tout 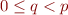 que
que 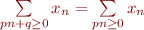 .
.
Rappelons notre règle pour la périodicité :
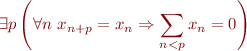
Nous l'avions imposé car si la suite 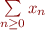 est périodique de période
est périodique de période 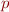 alors par stabilité :
alors par stabilité :
![Equation $$\[\begin{array}{r@{}l}
\sum\limits_{n \ge 0}x_n
&{} = \sum\limits_{n < p}x_n + \sum\limits_{n \ge p}x_n\\
&{} = \sum\limits_{n < p}x_n + \sum\limits_{n \ge 0}x_{n+p}\\
&{} = \sum\limits_{n < p}x_n + \sum\limits_{n \ge 0}x_n\\
\end{array}\]$$](/lib/exe/fetch.php?media=wiki:latex:/img9e005113ebc26984bdd3d9ebd90b0e1a.png)
Donc si 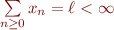 nous aurions
nous aurions 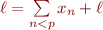 , donc il est nécessaire que
, donc il est nécessaire que 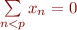 , comme c'est le cas par exemple pour
, comme c'est le cas par exemple pour 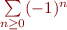 . L'idée était d'écarter notre meilleure ennemie
. L'idée était d'écarter notre meilleure ennemie 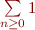 , mais nous venons de voir que plus généralement ce sont les
, mais nous venons de voir que plus généralement ce sont les 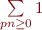 qui apparaissent.
qui apparaissent.
En effet, si 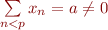 nous pouvons utiliser la somme pour obtenir
nous pouvons utiliser la somme pour obtenir 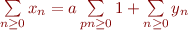 , où :
, où :
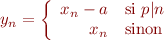
Ainsi, toute série périodique dont la tête 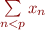 n'est pas nulle se décompose en la somme d'une série
n'est pas nulle se décompose en la somme d'une série 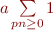 et d'une série dont la tête est nulle. Si on admet que les séries périodiques à tête nulle ont une valeur
et d'une série dont la tête est nulle. Si on admet que les séries périodiques à tête nulle ont une valeur  , alors il s'agit d'une sorte de forme indéterminée
, alors il s'agit d'une sorte de forme indéterminée  dont nous souhaitons seulement extraire les valeurs
dont nous souhaitons seulement extraire les valeurs  .
.
Le problème est que la somme n'est pas un opérateur clos pour les séries que nous souhaitons considérer. Ainsi, à partir de n'importe quelle série périodique il est possible de faire apparaître des formes indéterminées :
![Equation $$\[\begin{array}{r@{}l}
\sum\limits_{n \ge 0}x_n
&{} = \sum\limits_{0 \le q < p}\left(\sum\limits_{pn+q \ge 0}x_q\right)\\
&{} = \sum\limits_{0 \le q < p}\left(x_q\sum\limits_{pn+q \ge 0}1\right)\\
&{} = \sum\limits_{0 \le q < p}\left(x_q\sum\limits_{pn \ge 0}1\right)\\
&{} = \sum\limits_{pn \ge 0}1 \times \sum\limits_{0 \le q < p}x_q\\
\end{array}\]$$](/lib/exe/fetch.php?media=wiki:latex:/img7a1821be1aed95fa58274fdf8058ef50.png)
En particulier, si la tête 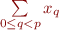 est nulle alors la série devrait valoir
est nulle alors la série devrait valoir  , ce qui est contradictoire avec des résultats comme
, ce qui est contradictoire avec des résultats comme 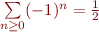 . Mais en fait, encore une nous reconnaissons ici une forme indéterminée
. Mais en fait, encore une nous reconnaissons ici une forme indéterminée  .
.
Interdire d'utiliser la somme sur les séries périodiques interdirait des calculs comme la première méthode pour calculer la série alternée des entiers. D'un autre côté, dans les exemples choisis je ne partais pas de deux séries acceptables pour aboutir à une série inacceptable, mais je partais d'une série acceptable que je décomposais en utilisant la somme en deux séries dont au moins l'une était inacceptable. Or, en notant  l'ensemble des séries acceptables (suivant notre critère de tête nulle si périodicité par exemple), la somme est définie de
l'ensemble des séries acceptables (suivant notre critère de tête nulle si périodicité par exemple), la somme est définie de 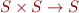 donc une telle décomposition n'est pas une opération valide.
donc une telle décomposition n'est pas une opération valide.
Ainsi, il n'y a pas (encore ?) contradiction, mais notez qu'il faut être bien prudent sur les opérations effectuées. En particulier, pour pouvoir utiliser l'heuristique de Ramanujan, il faudrait prouver que la dilatation de série 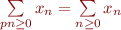 ne permet pas de faire apparaître des séries inacceptables. Et de façon plus générale, il faudrait s'assurer de la cohérence de nos règles en montrant qu'elles ne font pas apparaître non plus de séries inacceptables.
ne permet pas de faire apparaître des séries inacceptables. Et de façon plus générale, il faudrait s'assurer de la cohérence de nos règles en montrant qu'elles ne font pas apparaître non plus de séries inacceptables.
Séries inacceptables ?
J'ai retenu le critère de tête nulle si périodicité afin de pouvoir utiliser la stabilité sans problème, et par problème je veux dire tomber sur la même série en ayant rendu les équations incohérentes. Mais en fait c'est plutôt un problème d'auto-similarité. Par exemple, la série (non périodique, exercice ^^) 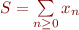 définie par :
définie par :
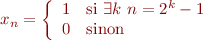
vérifie d'une part que si  est pair alors :
est pair alors :
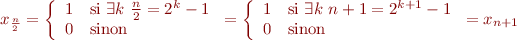
Note : nous avons bien 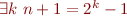 équivalent à
équivalent à 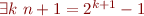 car le cas
car le cas  est impossible puisque
est impossible puisque  .
.
d'autre part, remarquons que  est pair si et seulement si
est pair si et seulement si  , et dans ce cas
, et dans ce cas 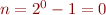 . Ainsi,
. Ainsi,  est le seul entier pair tel que
est le seul entier pair tel que  . Prenons à présent le cas où
. Prenons à présent le cas où  est impair, il s'écrit alors sous la forme
est impair, il s'écrit alors sous la forme 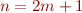 , donc
, donc 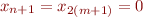 .
.
Pfiou ! Tout ça pour prouver que 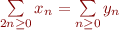 tel que :
tel que :
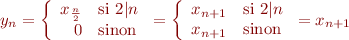
Donc :
![Equation $$\[\begin{array}{r@{}l}
S
&{} = \sum\limits_{n \ge 0}x_n\\
&{} = 1 + \sum\limits_{n \ge 1}x_n\\
&{} = 1 + \sum\limits_{n \ge 0}x_{n+1}\\
&{} = 1 + \sum\limits_{2n \ge 0}x_n\\
\end{array}\]$$](/lib/exe/fetch.php?media=wiki:latex:/img70f5db820c01f5dc1b3f88c890549982.png)
Ainsi, en utilisant la dilatation de série 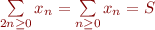 nous avons que
nous avons que 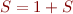 , ce qui nous offre un exemple de série inacceptable qui n'est pas périodique. Donc, si nous voulons utiliser l'heuristique de Ramanujan il faut reformuler le critère d'acceptabilité, et si nous nous passons de la dilatation de série il faut montrer que le critère de tête nulle si périodique est suffisant pour les lois de stabilité et de linéarité…
, ce qui nous offre un exemple de série inacceptable qui n'est pas périodique. Donc, si nous voulons utiliser l'heuristique de Ramanujan il faut reformuler le critère d'acceptabilité, et si nous nous passons de la dilatation de série il faut montrer que le critère de tête nulle si périodique est suffisant pour les lois de stabilité et de linéarité…
Sortir la tête du sable
Dans sa vidéo sur l'hypothèse de Riemann, El Jj m'a ouvert les yeux sur la fonction zêta de Riemann, qui peut être prolongée de manière unique de façon à donner des valeurs à certaines séries. Ainsi, 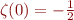 serait la bonne valeur pour ma meilleure ennemie la série
serait la bonne valeur pour ma meilleure ennemie la série 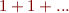 , qui ne devrait donc pas être considérée comme inacceptable. Mes préjugés m'ont aveuglé, aaah !
, qui ne devrait donc pas être considérée comme inacceptable. Mes préjugés m'ont aveuglé, aaah !
Dans les commentaires du premier billet de Science étonnante sur les séries divergentes, Matheux montre2) que la stabilité et la linéarité sont incohérents, en prenant la série qui m'a motivé depuis le début, à savoir 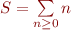 .
.
En effet, par stabilité,  , ou plus formellement en notant :
, ou plus formellement en notant :
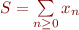 avec
avec 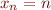
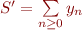 avec
avec 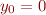 et
et 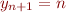
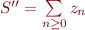 avec
avec 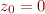 ,
,  et
et 
L'axiome de stabilité nous assure que  , d'où
, d'où 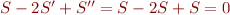 .
.
Mais par linéarité 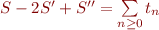 , où
, où 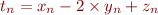 . Or :
. Or :
D'où par stabilité 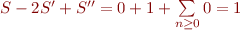 ! Ce qui contredit
! Ce qui contredit  .
.
En passant, 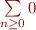 peut être obtenu par linéarité. En effet,
peut être obtenu par linéarité. En effet, 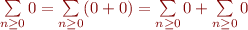 , d'où en retranchant
, d'où en retranchant 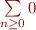 des deux côtés nous avons bien
des deux côtés nous avons bien 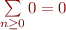 .
.
Ainsi, il faut choisir entre stabilité et linéarité… Matheux, en évoquant la convergence d'Abel avec 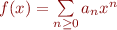 montre la voie à suivre : il faut garder la linéarité, qui respecte la structure de polynôme
montre la voie à suivre : il faut garder la linéarité, qui respecte la structure de polynôme 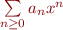 (que l'on retrouve aussi dans la représentation d'un nombre dans une base donnée… un rapport avec les nombres p-adiques ?). Extraire le premier terme revient à décaler la puissance :
(que l'on retrouve aussi dans la représentation d'un nombre dans une base donnée… un rapport avec les nombres p-adiques ?). Extraire le premier terme revient à décaler la puissance : 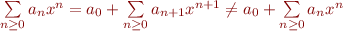 . C'est cela qui justifie la structure de liste (infinie, certes) que j'utilise depuis le début, et qui est responsable (voir le second billet de Science étonnante) de la perte de la commutativité de l'addition.
. C'est cela qui justifie la structure de liste (infinie, certes) que j'utilise depuis le début, et qui est responsable (voir le second billet de Science étonnante) de la perte de la commutativité de l'addition.
Note : Comparer la sommation d'abel avec celle de Dirichlet.
Le problème maintenant est sans la régularité ou la linéarité il devient difficile de faire des calculs… Peut-être qu'il existe des sous-classes des séries divergentes où seules certaines règles sont cohérentes. Ainsi, 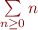 ne serait pas dans la classe des séries utilisant la stabilité et la linéarité, mais les séries géométriques si. Et
ne serait pas dans la classe des séries utilisant la stabilité et la linéarité, mais les séries géométriques si. Et 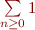 ne serait pas dans la classe des séries utilisant la stabilité car
ne serait pas dans la classe des séries utilisant la stabilité car 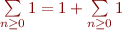 .Et ce serait intéressant du coup de caractériser les séries convergences parmi les familles des séries divergentes. Il faudra prouver que chaque classe de séries est close pour les règles de calcul qui y sont autorisées….
.Et ce serait intéressant du coup de caractériser les séries convergences parmi les familles des séries divergentes. Il faudra prouver que chaque classe de séries est close pour les règles de calcul qui y sont autorisées….
J'ai beaucoup apprécié l'approche de 3Blue1Brown pour vulgariser le processus de découverte/invention autour des séries divergentes.
Réponse à Science4All
Dans une de ses vidéos, Science4All montre que les suites définies par récurrence linéaire non barycentriques à une série convergente près peuvent être sommées de façon unique en respectant la linéarité, la stabilité et la régularité. De plus, il a défié la communauté de pouvoir prouver la réciproque, à savoir qu'il n'y a pas d'autre suite pouvant être sommée de façon unique par ces règles. Je pense avoir une preuve…
Prenons une suite 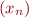 et supposons qu'il est possible en utilisant seulement ces trois règles de pouvoir déterminer une valeur unique à la série
et supposons qu'il est possible en utilisant seulement ces trois règles de pouvoir déterminer une valeur unique à la série  . Cela revient donc de passer de l'équation initiale
. Cela revient donc de passer de l'équation initiale  à l'équation
à l'équation 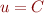 où
où  est une série convergente. Ensuite, par régularité une valeur réelle a pu être attribuée à la série divergente
est une série convergente. Ensuite, par régularité une valeur réelle a pu être attribuée à la série divergente 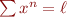 . Pour travailler avec les équations, nous ne nous autoriserons qu'à ajouter des deux côtés une même série, ou à multiplier chaque côté par un scalaire. Plus formellement, l'ensemble de règles utilisé est :
. Pour travailler avec les équations, nous ne nous autoriserons qu'à ajouter des deux côtés une même série, ou à multiplier chaque côté par un scalaire. Plus formellement, l'ensemble de règles utilisé est :
 où
où  est une série
est une série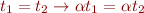 où
où  est un réel
est un réel
Comme nous partons de  pour arriver à
pour arriver à 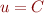 , le terme
, le terme 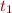 devra rester globalement constant. En fait, la seule succession d'opérations permettant de le modifier momentanément pour ensuite y revenir est :
devra rester globalement constant. En fait, la seule succession d'opérations permettant de le modifier momentanément pour ensuite y revenir est :
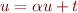

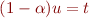
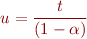
pour  , bien sûr. En effet, les autres possibilités avec les règles données ne permettent que de retomber sur l'équation de départ. En remontant depuis le résultat
, bien sûr. En effet, les autres possibilités avec les règles données ne permettent que de retomber sur l'équation de départ. En remontant depuis le résultat 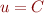 , cette succession d'opération ne permet que de faire apparaître plus haut une équation de la forme
, cette succession d'opération ne permet que de faire apparaître plus haut une équation de la forme  , donc une occurrence de la série avec un coefficient, et une série convergente.
, donc une occurrence de la série avec un coefficient, et une série convergente.
Les autres transformations ont été obtenues en modifiant le terme à droite. Nous supposons qu'il a été possible d'obtenir un résultat unique 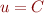 en partant de l'équation initiale
en partant de l'équation initiale  . Le membre droit construit pour arriver à ce résultat n'a pu utiliser que
. Le membre droit construit pour arriver à ce résultat n'a pu utiliser que  , des séries convergentes, des applications successives de
, des séries convergentes, des applications successives de  et la linéarité. Notamment, il n'y a qu'un nombre fini
et la linéarité. Notamment, il n'y a qu'un nombre fini  d'applications de
d'applications de  .
.
Notez que pour toutes suites  et
et  nous avons que
nous avons que 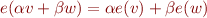 donc il est possible de faire rentrer les applications successives de
donc il est possible de faire rentrer les applications successives de  à l'intérieur des multiplications et sommes. De plus, les séries convergentes sont stables par linéarité et stabilité. Donc ce membre droit est nécessairement de la forme :
à l'intérieur des multiplications et sommes. De plus, les séries convergentes sont stables par linéarité et stabilité. Donc ce membre droit est nécessairement de la forme :

Il est peut-être possible d'arriver au même résultat de différentes façons, où nous récrivons les membres droits de la même manière. Parmi tous ces membres droits possibles, prenons en un tel que  est le plus petit possible. En passant,
est le plus petit possible. En passant,  , car sinon il aurait été possible d'obtenir un résultat uniquement par linéarité en partant de
, car sinon il aurait été possible d'obtenir un résultat uniquement par linéarité en partant de  et de séries convergentes, ce qui signifie que
et de séries convergentes, ce qui signifie que  devrait être une série convergente.
devrait être une série convergente.
Montrons par l'absurde que  . Nous obtenons donc l'équation
. Nous obtenons donc l'équation 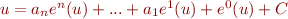 . Comme
. Comme 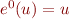 , nous pouvons soustraire
, nous pouvons soustraire  des deux côtés de l'équation pour obtenir que
des deux côtés de l'équation pour obtenir que 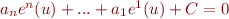 . Nous avons deux cas possibles :
. Nous avons deux cas possibles :
- Si
 alors en appliquant la stabilité nous avons que
alors en appliquant la stabilité nous avons que 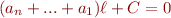 donc la série convergente vaut
donc la série convergente vaut  . Ainsi, l'équation
. Ainsi, l'équation 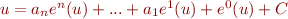 donne que
donne que  , ce qui ne renseigne en rien sur la valeur de
, ce qui ne renseigne en rien sur la valeur de  . Or, c'était cette équation qui était censé nous donner un résultat. D'où une contradiction.
. Or, c'était cette équation qui était censé nous donner un résultat. D'où une contradiction. - Si
 alors au moins l'un des
alors au moins l'un des  est non nul. Soit
est non nul. Soit  le plus petit des
le plus petit des  tel que
tel que  est non nul. Ainsi, nous obtenons une équation de la forme
est non nul. Ainsi, nous obtenons une équation de la forme 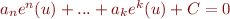 avec
avec  et
et  . Donc
. Donc  . En notant
. En notant 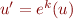 et
et 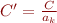 nous obtenons une nouvelle équation :
nous obtenons une nouvelle équation :

Or, par stabilité 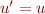 , donc cette équation permet d'obtenir le résultat avec seulement
, donc cette équation permet d'obtenir le résultat avec seulement 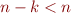 applications de
applications de  , ce qui contredit la minimalité de
, ce qui contredit la minimalité de  .
.
(Edit du 13/09 : En faisant remonter 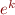 au dessus des séries convergentes et de la linéarité, cela revient à dire que
au dessus des séries convergentes et de la linéarité, cela revient à dire que  , donc en supposant que
, donc en supposant que 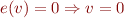 , nous avons bien
, nous avons bien  , et c'est cela qui contredit la minimalité de
, et c'est cela qui contredit la minimalité de  .)
.)
D'où  , et nous pouvons4) récrire l'équation :
, et nous pouvons4) récrire l'équation :
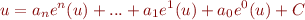
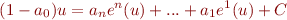
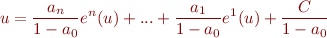
Dit autrement, en renommant les variables et en récrivant l'équation :

Ainsi, une telle suite est bien définie par récurrence linéaire. Il ne reste qu'à montrer par l'absurde que  . En effet, si
. En effet, si  alors par stabilité
alors par stabilité  donc
donc 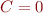 . Nous avons donc uniquement
. Nous avons donc uniquement 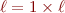 , ce qui ne permet en rien de trouver le résultat. Or, c'était cette équation qui était censée nous donner le résultat. D'où la contradiction attendue.
, ce qui ne permet en rien de trouver le résultat. Or, c'était cette équation qui était censée nous donner le résultat. D'où la contradiction attendue.
Ainsi, à moins d'une erreur dans mon raisonnement, les séries divergentes sommables de façon unique par linéarité, stabilité et régularité sont précisément les suites définies par récurrence linéaire non barycentriques à une série convergente près.
Notez que je restreins les moyens utilisables, car pour moi la question est de pouvoir caractériser l'ensemble des séries divergentes donnant des valeurs cohérentes en utilisant exactement ces trois règles. L'appel constant au constructivisme de la réponse peut cependant surprendre, et je serai ravi d'en discuter dans les commentaires de la vidéo ;)
 consiste à rajouter un zéro devant la suite.
consiste à rajouter un zéro devant la suite. à cause du
à cause du  au lieu du
au lieu du  dans le membre de gauche.
dans le membre de gauche.
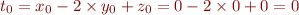
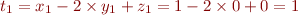
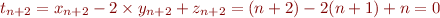
 où
où  est obtenu par linéarité à partir de
est obtenu par linéarité à partir de  , ou
, ou